There’s a claim about snowflakes that’s repeated so often it starts to feel axiomatic: no two are alike. It’s one of those facts that sits quietly in the back of your mind. You don’t question it. You just accept it, file it away, and move on.
I don’t remember where I heard it first, but the more I thought about it, the more suspicious I felt. Snowflakes form under broadly similar conditions, they follow the same physical laws, so why should every single one turn out differently? At some point, surely, nature should repeat itself?
Science behind the symmetry
To understand why snowflakes have such a rigid symmetry, we have to zoom right down to the scale of individual water molecules. A water molecule, (H₂O) has two hydrogen atoms forming an angle of 104.5° around the oxygen.
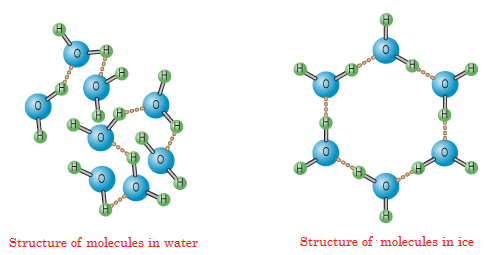
This geometry determines how water molecules interact when they come close together. Water molecules are polar, i.e. the oxygen carries a negative charge, and the hydrogen ends carry a positive charge, which allows neighbouring molecules to form hydrogen bonds. Each water molecule can form up to four hydrogen bonds- two through its hydrogen atoms and two through lone pairs on the oxygen. These bonds are much weaker than covalent bonds, but strong enough to impose structure when many molecules come together.
When water freezes under normal atmospheric conditions, these hydrogen bonds and settle into a lattice where each molecule bonds to four neighbours in a roughly tetrahedral configuration. And then when this 3D structure is projected into the plane perpendicular to the crystal’s main axis, it naturally produces hexagonal symmetry. Once this lattice begins to form, the symmetry is locked in. Any additional water vapour that freezes onto the crystal must attach itself in a way that preserves the existing hydrogen-bond network. This molecular geometry also explains why real1 snowflakes always have six arms.
‘No Two Are Alike’
Something I find particular elegant is that symmetry alone doesn’t determine a snowflake’s final appearance. While the lattice enforces hexagonal symmetry, it doesn’t prescribe how fast each arm grows or how often it branches, because that depends on the environment through which the snowflake falls.
As a snowflake moves through a cloud, it encounters constantly changing temperature and humidity. At slightly warmer temperatures, growth tends to favour thin plates. At colder temperatures, column like structures dominate and small fluctuations in humidity can cause one arm to grow marginally faster than the others. And because growth changes how air flows around the crystal, that tiny difference feeds back into the system. Fascinatingly,, this still doesn’t break the symmetry as each arm experiences roughly the same environmental conditions at the same time, so they tend to branch in similar2 ways.

Scientifically speaking, the number of possible branching patterns, growth histories, and environmental trajectories is unsurprisingly beyond comprehension. Even if two snowflakes began growing in nearly identical conditions, minute differences in molecular attachment or airflow would push them onto different paths almost immediately.
A particularly good explanation comes from this Veritasium video, the source of most the things mentioned here, which looks at how snowflakes grow under controlled conditions. What’s striking is that even when temperature and humidity are held almost constant, snowflakes still refuse to repeat themselves.
However, I find that focusing too hard on whether the claim is literally true somewhat misses the point. I find it a remarkable thing isn’t that snowflakes are unique, it’s that they’re unique despite being so constrained. Every snowflake obeys the same geometry, the same chemistry, the same physical laws, and yet, within those rules, there’s room for endless variation.
With Christmas so close, it feels like a good time to slow down and notice the small things again. Snowflakes don’t rush to be impressive, they just follow the rules of nature and grow, one layer at a time. Whether you’re revising or resting, I hope you get a bit of space over the holidays to do the same. Merry Christmas for when it arrives! As usual – find attached some of my favourite festive xkcd comics.



- It’s vital to emphasise this because if you’ve ever seen snowflakes with octagonal symmetry on the web, know that an eightfold snowflake would require a completely different bonding geometry which water molecules simply cannot sustain. ↩︎
- Note that “similar” is not “identical”. The overall pattern remains six-fold, while the fine details diverge. ↩︎