It’s getting to that time of the semester again, the part where your brain is somewhere between tired and trying its best, and every test paper starts to look the same. And sometimes, when I’m staring at an exam I’m meant to be focusing on, my mind wanders into questions that have nothing1 to do with the module I’m sitting.
The other day, one such thought hit me: why is this sheet of paper, this exact A4 sheet in front of me, the size it is? Why 297 × 210 mm? Why not a nice round 300 × 200? Why not squares?
A4 is everywhere from worksheets, lecture notes, problem sheets, printer trays, so if we use it constantly, surely there must be a reason for its exact shape. And even then, what does the ‘A’ even stand for in A4? Are there B4s and C4s? (Spoiler: Yes)
What the ‘A’ in A4 stands for…
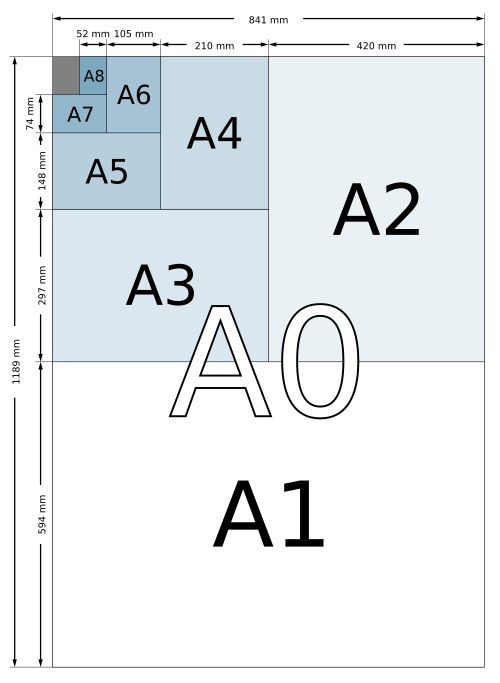
The A-series comes from the ISO 216 paper standard, essentially an international agreement on how big paper should be so that printers, folders, envelopes, textbooks, photocopiers all play nicely together.
Everything in the A-series is built on one mathematical requirement: when we cut the paper in half, the halves must have the same shape as the original. Think of it like a fractal2 but rectangular.
So the A0 is defined to have an area of exactly 1 m2. So everything we go up a number (A1, A2, A3), we halve the area. So A4 in then simply half of A3, which is half of A2.. all the way down to A0.
Ratios
Imagine we’re designing a universal paper system where we want:
- A0 – cut in half -> two A1s
- A1 – cut in half -> two A2s
- …
- All of them have the same shape
For rectangles to have neatly but stay the “similar”, the aspect ratio (aka the ratio of the width to the height) has to satisfy:
L/W = W/(L/2)
Simplifying this we get:
L/W = √2
Hence, the only aspect ratio that stays the same when we cut a paper in half is √2 : 1
So if we start with A0 which has area 1 m2 and take the ratio to be √2 : 1, we can calculate its sides:
- Long side: 2^(1/4) m ≈ 1189 mm
- Shor side: 2^(-1/4) m ≈ 841 mm
Then following the halving process:
- A1 = 842 × 594 mm
- A2 = 594 × 420 mm
- A3 = 420 × 297 mm
- A4 = 297 × 210 mm
And that’s how we get the dimensions of 297 × 210 mm for the A4 paper!
We can also express the entire A-series as the geometric series:
An = 2-n/2 × A0
Then A4 = 2-4/2 × A0 = 2-2 × A0 = 1/4 A0
Which tells us that A4 is one quarter of A0
Note on the ‘B’ and ‘C’ series
The B-series are like the in-between sizes, so it’s geometrically halfway between An and An-1. For instance, a B4 would a paper size between A3 and A4. They are more commonly used in posters, passports, magazines and anything that needs a bit more breathing rom than the A-series allows.
The C- series are designed for envelopes. For an experiment to see for yourself, take an A4 sheet and fold it, you’ll find that a C4 envelop perfectly fits an A4 sheet without bending. So it uses the geometric mean of the A and B series to make an envelope that’s just right.
So the next time you’re procrastinating mid exam and ever wonder why the paper is this exact size, well, now you know. It’s maths, it’s always maths.
