It was around this time, three years ago, that I first heard the words “Paranormal Distribution” on a Teams call.
So in the spirit1 of Halloween, here’s a brief exploration of the Paranormal Distribution, a (super)natural extension of the Gaussian model that describes data unexplainable by conventional statistics.
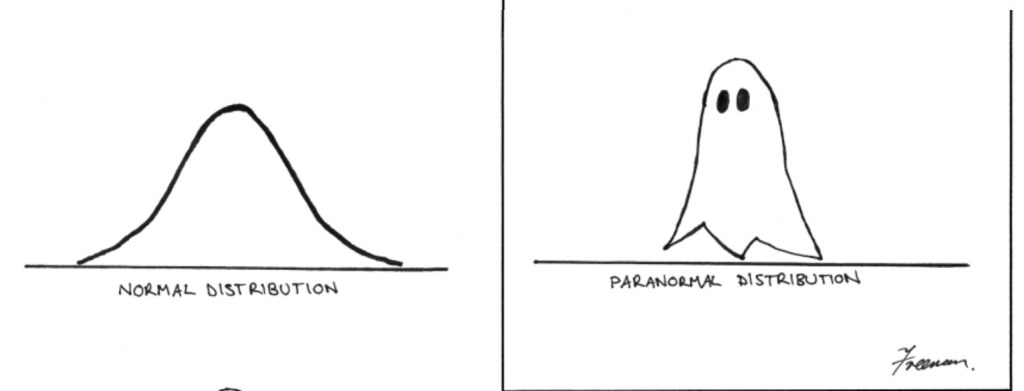
The normal distribution, or Gaussian curve, underpins much of statistics. Everything from exam scores to measurement errors and height of pumpkins (probably) can be described by it.
Mathematically, it’s probability density function is given by:
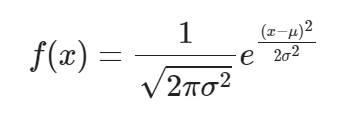
Where µ is the mean (average), δ is the standard deviation (how spread out the data is), and nothing weird happens… yet
In this post, I propose the probability density function for a random variable X to follow a Paranormal Distribution2, given by:
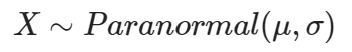
Similar to the normal distribution, this has two parameters, but behaves rather differently under observation:
- µ is the mean location of haunting
- δ is the spread of disturbances (or the spectral deviation)
Now as with any distribution, we need a probability density function3
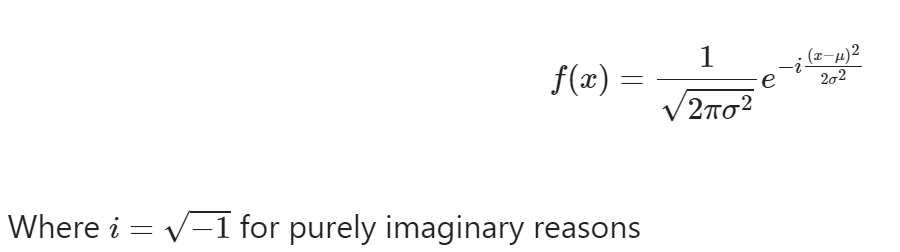
In conclusion, the paranormal distribution offers a rather compelling framework for modelling distributions that cannot be explained by real datasets. While further work and experiments are certainly required to verify its spectral stability and convergence properties, initial results suggest a significant4 presence of something. So may your models stay peaceful, and if they don’t, at least you now know a model for it.
I had a fair bit of fun writing this post, and I hope you did reading too! Happy Halloween, until next time!

- Pun intended ↩︎
- The image below can be found from on this page ↩︎
- The proof of the derivation of this left as an exercise to the reader. On the other hand… I intend to write a future post on the appearance of complex numbers in statistical modelling ↩︎
- And no I will be not be conducting a hypothesis using this distribution.. yet ↩︎